
Pengertian Standar Deviasi
Standar deviasi merupakan perhitungan statistik yang mengukur sebaran data terhadap nilai rata-ratanya. Secara teoritis, nilai simpangan baku tidak pernah negatif (non-negative).
Semakin besar nilainya, maka mengindikasikan bahwa sebaran data semakin jauh dari nilai rata-rata. Sebaliknya, semakin kecil nilai standar deviasi mengindikasikan bahwa data tersebar di sekitar nilai rata-rata.
Perhatikan kurva berikut untuk lebih memahami konsep standar deviasi.
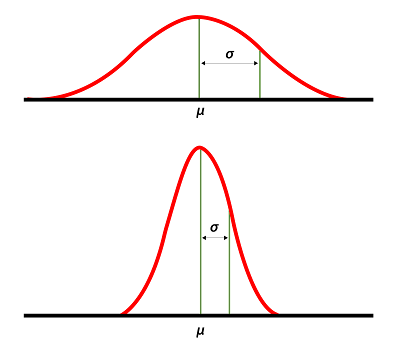
Berdasarkan gambar di atas, terdapat dua simbol yaitu $\mu$ yang berarti nilai rata-rata data dan $\sigma$ yang merupakan nilai standar deviasi.
Perhatikan, pada gambar bagian atas bentuk kurva yang terbentuk cenderung melebar sehingga simpangan baku $\sigma$ relatif lebih besar jika dibandingkan dengan gambar bagian bawah.
Sehingga, melalui ilustrasi gambar tersebut kita sudah bisa membayangkan kondisi dari nilai standar deviasi suatu data.
Fungsi Standar Deviasi
Sejatinya, fungsi mengetahui simpangan baku sudah bisa diketahui setelah kita mengetahui definisi dan ilustrasi sebelumnya.
Nilai standar deviasi berfungsi untuk melihat seberapa jauh sebaran data terhadap nilai rata-ratanya.
Dalam statistik, hal ini sangat penting mengingat dengan mengetahui nilai rata-rata dan simpangan baku nya, kita bisa menggambarkan populasi data melalui sampel data saja tanpa perlu melakukan pengumpulan data populasi secara keseluruhan.
Contoh sederhana, misalnya Anda hendak melakukan penelitian berapa kira-kira tinggi badan siswa kelas 12.
Dalam kasus ini, Anda tidak perlu melakukan pengukuran terhadap seluruh siswa kelas 12 tersebut. Melainkan cukup dengan mengambil sampel siswa dari setiap kelas saja, lalu hitung rata-rata dan standar deviasinya. Maka kita bisa mengetahui kira-kira tinggi badan siswa kelas 12 secara keseluruhan.
Rumus Standar Deviasi
Terdapat dua rumus untuk menghitung standar deviasi. Pertama, rumus perhitungan untuk data populasi. Kedua, rumus untuk kasus data sampel.
Namun sebelum ke rumus perhitungan simpangan baku, alangkah baiknya Anda mengetahui dan memahami statistik dasar mengenai rumus mean atau rata-rata.
1. Populasi
Jika Anda memiliki data set berupa populasi bukan sampel, maka gunakanlah rumus simpangan baku populasi berikut.
$\sigma = \sqrt{\frac{\sum_{i=1}^N (x_i - \mu)^2}{N}}$ ...(1)
$\sigma =$ standar deviasi populasi
$N =$ jumlah populasi data
$x_i =$ data ke-i
$\mu =$ nilai rata-rata populasi data
2. Sampel
Sebaliknya, jika Anda tidak memiliki data populasi, melainkan hanya sampel data saja yang diambil, maka gunakanlah rumus simpangan baku sampel berikut.
$s = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}$ ...(2)
$s =$ standar deviasi sampel
$n =$ jumlah sampel data
$x_i =$ data ke-i
$\bar{x} =$ nilai rata-rata sampel data
